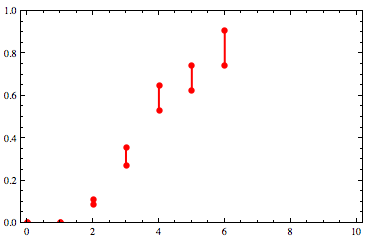
I have some constraints on a CDF in the form of a list of x-values and for each x-value, a pair of y-values that the CDF must lie between. We can represent that as a list of {x,y1,y2} triples such as

constraints = {{0, 0, 0}, {1, 0.00311936, 0.00416369}, {2, 0.0847077, 0.109064}, 
 {3, 0.272142, 0.354692}, {4, 0.53198, 0.646113}, {5, 0.623413, 0.743102}, 
 {6, 0.744714, 0.905966}}

Graphically that looks like this:

And since this is a CDF there's an additional implicit constraint of

{Infinity, 1, 1}

Ie, the function must never exceed 1. Also, it must be monotone.

Now, without making any assumptions about its functional form, we want to find a curve that respects those constraints. For example:

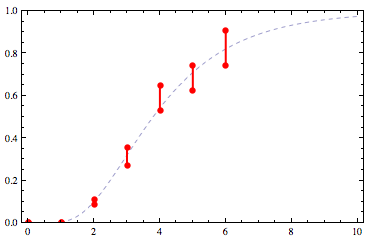
(I cheated to get that one: I actually started with a nice log-normal distribution and then generated fake constraints based on it.)

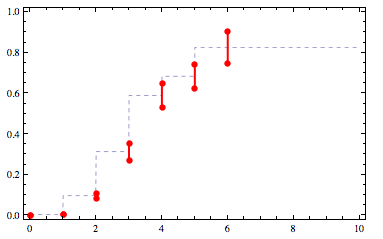
One possibility is a straight interpolation through the midpoints of the constraints:

mids = ({#1, Mean[{#2,#3}]}&) @@@ constraints
f = Interpolation[mids, InterpolationOrder->0]

Plotted, f looks like this:

That sort of technically satisfies the constraints but it needs smoothing. We can increase the interpolation order but now it violates the implicit constraints (always less than one, and monotone):

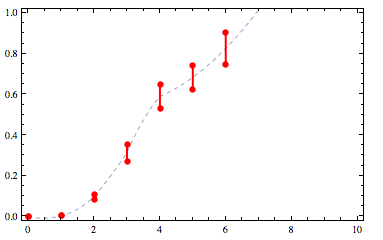
How can I get a curve that looks as much like the first one above as possible? Note that NonLinearModelFit with a LogNormalDistribution will do the trick in this example but is insufficiently general as sometimes there will sometimes not exist a log-normal distribution satisfying the constraints.