Consider the set of non-decreasing surjective (onto) functions from (-inf,inf) to [0,1]. (Typical CDFs satisfy this property.) In other words, for any real number x, 0 <= f(x) <= 1. The logistic function is perhaps the most well-known example.

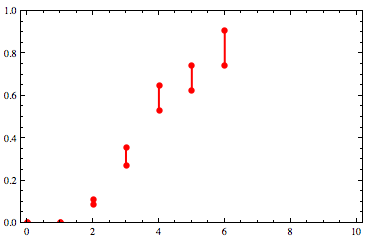
We are now given some constraints in the form of a list of x-values and for each x-value, a pair of y-values that the function must lie between. We can represent that as a list of {x,ymin,ymax} triples such as

constraints = {{0, 0, 0}, {1, 0.00311936, 0.00416369}, {2, 0.0847077, 0.109064}, 
 {3, 0.272142, 0.354692}, {4, 0.53198, 0.646113}, {5, 0.623413, 0.743102}, 
 {6, 0.744714, 0.905966}}

Graphically that looks like this:

We now seek a curve that respects those constraints. For example:

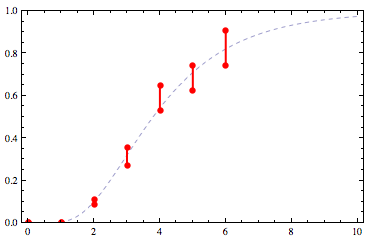
Let's first try a simple interpolation through the midpoints of the constraints:

mids = ({#1, Mean[{#2,#3}]}&) @@@ constraints
f = Interpolation[mids, InterpolationOrder->0]

Plotted, f looks like this:

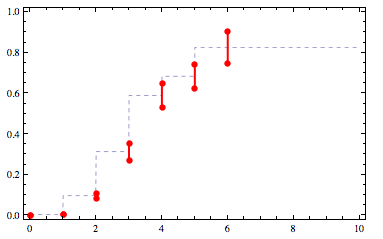
That function is not surjective. Also, we'd like it to be smoother. We can increase the interpolation order but now it violates the constraint that its range is [0,1]:

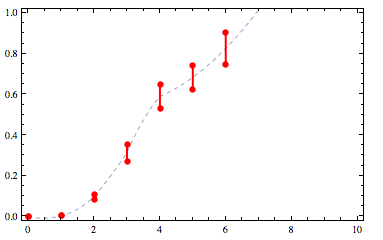
The goal, then, is to find the smoothest function that satisfies the constraints:

1. Non-decreasing.
2. Tends to 0 as x approaches negative infinity and tends to 1 as x approaches infinity.
3. Passes through a given list of y-error-bars.

The first example I plotted above seems to be a good candidate but I did that with Mathematica's FindFit function assuming a lognormal CDF. That works well in this specific example but in general there need not be a lognormal CDF that satisfies the constraints.