Sampling uniformly at random from an n-dimensional unit simplex is the fancy way to say that you want n random numbers such that

• they are all non-negative,
• they sum to one, and
• every possible vector of n non-negative numbers that sum to one are equally likely.

In the n=2 case you want to sample uniformly from the segment of the line x+y=1 (ie, y=1-x) that is in the positive quadrant. In the n=3 case you're sampling from the triangle-shaped part of the plane x+y+z=1 that is in the positive octant of R3:

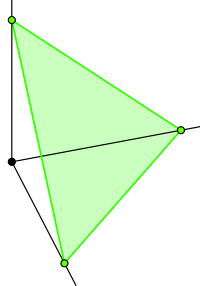
(Image from http://en.wikipedia.org/wiki/Simplex.)

Note that picking n uniform random numbers and then normalizing them so they sum to one does not work. You end up with a bias towards less extreme numbers.

Similarly, picking n-1 uniform random numbers and then taking the nth to be one minus the sum of them also introduces bias.

Wikipedia gives two algorithms to do this correctly: http://en.wikipedia.org/wiki/Simplex#Random_sampling (Though the second one currently claims to only be correct in practice, not in theory. I'm hoping to clean that up or clarify it when I understand this better. I initially stuck in a "WARNING: such-and-such paper claims the following is wrong" on that Wikipedia page and someone else turned it into the "works only in practice" caveat.)

Finally, the question: What do you consider the best implementation of simplex sampling in Mathematica (preferably with empirical confirmation that it's correct)?

Related questions

• http://stackoverflow.com/questions/2171074/generating-a-probability-distribution
• http://stackoverflow.com/questions/3007975/java-random-percentages